โดย ทีปานิส ชาชิโย
เมื่อทำการวิเคราะห์พฤติกรรมหรือทำนายสมบัติของระบบ อาทิเช่น แก็สที่อยู่ภายในลูกสูบเครื่องยนต์ น้ำที่อยู่ภายในแก้ว หรือแท่งโลหะสักชิ้น พลังงานของระบบ ถือเป็นตัวแปรสำคัญในการกำหนดสภาวะและคุณสมบัติของมัน ดังนั้นในบทนี้เราจะได้ศึกษาธรรมชาติของพลังงานภายในของระบบ ว่ามันสามารถมีค่าเพิ่มขึ้นหรือลดลงด้วยกระบวนการใดบ้าง
พิจารณาระบบของแก็ส ที่ประกอบด้วย 100 อนุภาคบรรจุอยู่ภายใน ซึ่งในความเป็นจริงข้อสรุปของการวิเคราะห์ในครั้งนี้ ใช้ได้โดยทั่วไปกับวัสดุหรือระบบทุกรูปแบบ แต่การยกตัวอย่างของแก็สในภาชนะ จะทำให้สามารถมองเป็นระบบได้เป็นรูปธรรมที่ชัดเจนมากขึ้น จากภาพจะเห็นว่าระบบมีพลังงานภายในอยู่น้อยมาก สังเกตได้จากการเคลื่อนที่ของแต่ละอนุภาคที่มีความเร็วค่อนข้างน้อย ประเด็นคำถามในที่นี้ก็คือ "เราจะเพิ่มพลังงานภายในของระบบ ด้วยกระบวนการใดได้บ้าง ?"
กระบวนการแรกที่เราคุ้นเคย ก็คือให้ความร้อนกับมัน ดังจะเห็นได้จากภาพที่เราเริ่มจุดไฟด้านล่าง ทำให้พลังงานในรูปของความร้อนไหลเข้าไปในระบบ ส่งผลให้พลังงานภายใน มีค่าเพิ่มขึ้น ซึ่งสามารถเขียนในรูปของสมการได้ว่า
นั่นหมายถึง พลังงานภายในของระบบ ที่เพิ่มขึ้น ก็มีค่าเท่ากับความร้อน \$dQ\$ ที่ไหลเข้าไปในระบบ จะสังเกตเห็นได้ว่า อนุภาคที่อยู่ในภาชนะ มีการเคลื่อนที่อย่างรวดเร็ว หรืออีกนัยหนึ่ง มันมีพลังงานจลน์เพิ่มขึ้น ซึ่งก็มาจากความร้อนที่ป้อนเข้าไปนั่นเอง
กระบวนการที่สอง ซึ่งสามารถเพิ่มพลังงานภายในให้กับระบบ ก็คือการ "ทำงานกับมัน" เมื่อพูดถึงงานที่ทำกับระบบ อาจจะดูเป็นนามธรรมที่เข้าใจยากอยู่บ้าง แต่ถ้าสังเกตตัวอย่างในภาพ ก็คือการที่เราออกแรงผลัก ผนังของของภาชนะ หรือผลักลูกสูบให้มีขนาดเล็กลง เมื่อออกแรงผลัก \$F\$ และออกแรงเป็นระยะทาง \$dx\$ ในทางฟิสิกส์ ก็คือการที่ตัวหุ่นยนต์ กำลังทำงาน \$dW=F dx\$ และงานอันนี้เอง ก็จะถ่ายเทเป็นพลังงานเข้าสู่ระบบ ทำให้อนุภาคในภาชนะ มีการเคลื่อนที่เร็วขึ้นดังแสดงในภาพ การที่เราเพิ่มพลังงานภายในระบบ จาก "งาน" ที่สิ่งแวดล้อมกระทำกับมัน สามารถเขียนให้อยู่ในรูปของสมการได้ว่า
ระบบในกรณีทั่วไปนั้น กระบวนการถ่ายเทพลังงานเข้าสู่ระบบ จะเกิดขึ้นได้จาก 2 ปัจจัยนี้เท่านั้น ก็คือความร้อนที่ถ่ายเทเข้าไป และงานที่เราทำกับมัน นี้เองคือกฎข้อที่ 1 ของ Thermodynamics ซึ่งเขียนให้กระชับอยู่ในรูปของสมการก็คือ
ยกตัวอย่างเช่น ระบบที่เรากำลังพิจารณาก็คือกาแฟสักแก้ว ครั้นเมื่อเติมน้ำพอสมควร น้ำตาล และผงเนยเทียมผงกาแฟหอมกรุ่นแล้ว ปรากฏว่าคุณสังเกตเห็นมันยังไม่ละลาย เราต้องการเพิ่มพลังงานภายในให้กับระบบ ด้วยหวังว่ามันจะละลายเข้ากันได้ดีขึ้น ซึ่งสามารถทำได้สองวิธี คือ 1) นำไปต้มอีกครั้งบนเตา นี้เองคือการเพิ่มพลังงานด้วยกระบวนการของ \$dQ\$ ซึ่งหากยังไม่เพียงพอ 2) เราก็สามารถออกแรงคนด้วยช้อน อันเป็นการ "ทำงาน" กับระบบ นี้เองคือการเพิ่มพลังงานด้วยกระบวนการของ \$dW\$
หมายเหตุ: หนังสือเรียนฟิสิกส์ในอดีต นิยามงาน \$dW\$ ว่าเป็นงานที่ "ระบบทำ" ซึ่งตรงกันข้ามในกรณีของเรา ที่เป็นงานซึ่ง "กระทำกับระบบ" ด้วยเหตุนี้ กฎข้อ 1 ของ Thermodynamics จึงเขียนอยู่ในรูป \$dU = dQ - dW\$ นี้เป็นเพียงความแตกต่างในเชิงคำนิยาม อันทำให้เครื่องหมายสลับกันจากบวกเป็นลบ อย่างไรก็ตาม แบบเรียนฟิสิกส์ในปัจจุบัน อาทิเช่น Serway, "College Physics" 9th Edition (และที่ใช้ในวิชาเคมีมาโดยตลอด) เริ่มมีการปรับมาใช้คำนิยามของ \$dW\$ ตรงกันกับที่เราใช้อยู่นี้
ตัวอย่างโจทย์
แก็สที่เรียกว่า mono-atomic ideal gas ปริมาณ 0.1 โมล โดนขังอยู่ในลูกสูบที่เคลือบด้วยฉนวนความร้อน มีแรงลัพธ์ (รวมทั้งจากความดันบรรยากาศ) กดลิ้นลูกสูบด้วยแรง 200 N อย่างต่อเนื่อง เมื่อกดเข้าไปได้เป็นระยะทาง 10 cm อุณหภูมิของแก็สจะเพิ่มขึ้นเท่าใด ?
วิธีทำ จากในบทที่หนึ่ง ระบบของแก็สในอุดมคติซึ่งโมเลกุลประกอบด้วยอะตอมเพียงอันเดียว หรือที่เรียกว่า mono-atomic ideal gas นั้น อุณหภูมิของมันแปรผันตรงกับพลังงานภายในของระบบ กล่าวคือ
| \$U = \frac{3}{2}Nk_B T\$ หรือ \$dU = \frac{3}{2}Nk_B dT\$ | --------- (E.1) |
เพราะฉะนั้นหากเราสามารถคำนวณหาพลังงาน \$dU\$ ที่เพิ่มขึ้นจากการออกแรงกดลิ้นลูกสูบ โดยอาศัยกฎข้อ 1 ของ Thermodynamics เราก็สามารถคำนวณหาอุณหภูมิที่เพิ่มขึ้น ดังที่โจทย์ต้องการทราบ
จากกฎข้อ 1 ของ Thermodynamics
โจทย์กำหนดให้ ภาชนะมีฉนวนความร้อนเคลือบอยู่ นั่นหมายความว่า ในกรณีนี้ความร้อนไม่สามารถไหลเข้าหรือออกจากระบบได้ กล่าวคือ \$dQ=0\$ ทำให้ในโจทย์ข้อนี้ \$dU=dW\$
เราสามารถคำนวณงาน \$dW\$ ที่สิ่งแวดล้อมกระทำแก็สได้ นั่นคือแรง \$F = 200N\$ และระยะทาง \$d = 10\,cm = 0.1\,m\$ ทำให้งานที่กระทำกับระบบก็คือ \$dW = Fd = 200 \times 0.1 = 20\,J\$ และงาน 20 จูลนี้เองเข้าไปทำให้พลังงานภายในของแก็สเพิ่มขึ้น \$dU = 20\,J\$
ย้อนกลับไปที่สมการ (E.1) \$dU = \frac{3}{2}Nk_B dT\$ ซึ่ง \$N\$ คือจำนวนโมเลกุลภายในภาชนะ ซึ่งโจทย์บอกว่ามีค่าเท่ากับ 0.1 โมล ดังนั้น \$N = 0.1\,N_A\$ เมื่อ \$N_A \$ คือ Avogadro Number ซึ่งมีค่าเท่ากับ \$6.02 \times 10^{23} \$ เพราะฉะนั้น
เทอม \$N_A k_B \$ นั้นก็คือ ค่าคงที่ซึ่งเรียกว่า Gas Constant \$N_A k_B \equiv R = 8.31\,J/K \cdot mol\$ ผนวกกับ \$dU = 20\,J\$ ดังนั้น
ในการวิเคราะห์พลังงานภายใน \$dU\$ ที่เพิ่มขึ้น อันเป็นผลมาจากความร้อนและงาน นั้นจำเป็นต้องมีความรอบคอบเมื่อพิจารณาเครื่องหมายของ \$dQ\$ และ \$dW\$
ในกรณีของ \$dQ\$ นิยามเป็นความร้อนที่ไหลเข้าสู่ระบบ กล่าวคือหาก \$dQ\$ มีค่าเป็นบวก นั้นแสดงว่าอุณหภูมิของสิ่งแวดล้อมนั้นมีค่าสูงกว่าระบบ ทำให้ความร้อนมีการไหลเข้าไปภายใน อาทิเช่นการเปิดเตาแก็สเพื่อต้มน้ำ อุณหภูมิของเปลวไฟที่สูงมากส่งผลให้ความร้อนไหลเข้าสู่กาต้มน้ำ แต่หาก \$dQ\$ มีค่าติดลบ นี้หมายถึงความร้อนกำลังถูกทำให้รั่วไหลออกจากตัวระบบ เข้าสู่สิ่งแวดล้อม อาทิเช่นขณะคุณกำลังอาบน้ำ อุณหภูมิของร่ายกายที่สูงกว่า ส่งผลให้ความร้อนไหลออกไปสู่น้ำเย็นที่อยู่โดยรอบ
ในกรณีของ \$dW\$ โดยนิยามแล้ว คืองานที่ "สิ่งแวดล้อม" กระทำกับระบบ อาทิระบบคือแก็สที่อยู่ในภาชนะ เรา (ในฐานะสิ่งแวดล้อม) ออกแรงบีบแก็สให้มีปริมาตรเล็กลง นี้เรียกว่างานมีค่าเป็นบวก และงานที่สิ่งแวดล้อมกระทำนี้ มีผลให้พลังงานภายในของระบบเพิ่มขึ้น แต่ในหลายกรณี \$dW\$ มีค่าติดลบซึ่งเราจะได้เห็นในตัวอย่างโจทย์ต่อไปนี้
ตัวอย่างโจทย์
Mono-atomic ideal gas ปริมาณ 0.2 โมล ณ ความดันบรรยากาศ อยู่ในภาชนะทรงกระบอก (พื้นที่หน้าตัด A = 10 ตารางเซนติเมตร) ใน 2 ลักษณะ คือ a) ปิดสนิท และ b) มีลิ้นลูกสูบให้ขยาย ออกอีกได้ 10 cm ดังแสดงในภาพ เมื่อให้ความร้อนเข้าไปช้าๆ รวมทั้งสิ้น 20 จูล อุณหภูมิของแก็สในภาชนะทั้ง 2 กรณี จะเพิ่มขึ้นเท่าๆกันหรือไม่ เพิ่มขึ้นเท่าใด ?
วิธีทำอีกเช่นเคย เราเริ่มจากความสัมพันธ์ระหว่างพลังงานภายในของแก็สกับอุณหภูมิของมัน นั่นคือ
| \$ U = \frac{3}{2}Nk_B T = \frac{3}{2}n\underbrace {N_A k_B }_{ \equiv R}T = \frac{3}{2}nRT \$ หรือ \$dU = \frac{3}{2}nRdT\$ | --------- (E.1) |
ในสมการข้างต้น เพื่อความสะดวกเราเขียนจำนวนของอนุภาคในภาชนะ ให้อยู่ในรูปจำนวนโมล \$N = nN_A \$ ทั้งนี้เพราะข้อมูลที่โจทย์กำหนดให้ก็คือ \$ n = 0.2\,{\text{mol}} \$
เนื่องจากในทั้งสองกรณี a ) และ b) มีลักษณะของภาชนะที่แก็สบรรจุอยู่แตกต่างกัน แม้ว่าให้ความร้อนเข้าไป 20 J เท่ากัน จะส่งผลให้พลังงานงานภายในเพิ่มขึ้นได้แตกต่างกัน
กรณี a) เมื่อพิจารณากฎข้อ 1 ของ Thermodynamics
โจทย์กำหนดให้ ภาชนะปิดสนิทมีปริมาตรคงที่ "งาน" ก็คือแรงคูณระยะทาง แม้ว่าสิ่งแวดล้อมภายนอกจะออกแรงบีบ เนื่องมาจากความดันบรรยากาศ แต่ไม่มีการเคลื่อนที่เพราะไม่สามารถกดให้ภาชนะ หรือปริมาตรของแก็สเล็กลงอีกได้ ดังนั้นในกรณี a) \$dW=0\$ มีผลทำให้ \$dU=dQ\$
จากโจทย์ \$dQ=20 J\$ ผนวกกับสมการ (E.1) ทำให้เราเขียนได้ว่า
กล่าวคือ อุณหภูมิของแก็สในกรณี a) จะเพิ่มขึ้น 8.02 เคลวิน ตอบ
กรณี b) เริ่มด้วยการพิจารณากฎข้อ 1 ของ Thermodynamics อีกครั้ง
นี้ต่างจากในกรณีแรก เพราะภาชนะเป็นลูกสูบที่เปิดโอกาส ให้มีการขยายตัวได้ หรือลิ้นลูกสูบมีการเคลื่อนที่ ดังนั้นเราต้องพิจารณาแรงที่สิ่งแวดล้อมกระทำกับระบบ และระยะทางของการเคลื่อนที่ เพื่อคำนวณหางาน \$ dW \$
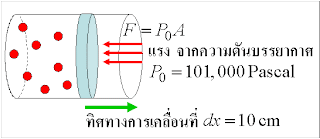
จากภาพจะเห็นว่า แรงที่สิ่งแวดล้อมภายนอกกระทำนั้น ก็เนื่องมาจากความดันบรรยากาศ สมมุติให้พื้นที่ของลิ้นลูกสูบมีค่าเป็น A ดังนั้นแรง ซึ่งคือผลคูณของความดันและพื้นที่รองรับ ก็คือ
แก็สเมื่อทำให้ร้อน มันย่อมขยายตัวออก ส่งผลให้ลิ้นลูกสูบเคลื่อนที่เป็นระยะทาง \$dx = 10\,cm = 0.1\,m \$ และงานที่สิ่งแวดล้อมกระทำก็คือ
ให้สังเกตว่างานในที่นี้ติดลบ ในทางคณิตศาสตร์ ก็เพราะว่าทิศทางการเคลื่อนที่ นั้นตรงกันข้ามกับทิศทางของแรงที่กระทำ ในทางฟิสิกส์ หมายถึงพลังงานกำลังสูญเสียออกจากระบบสู่สิ่งแวดล้อมนั่นเอง
เมื่อเราทราบว่า \$dW = - 10.1\,J\$ ทำให้สามารถคำนวณพลังงานภายในของแก็สที่เพิ่มขึ้นได้ว่า
จากนั้น อาศัยสมการ (E.1) เพื่อโยงความสัมพันธ์ไปยังอุณหภูมิที่เพิ่มขึ้น
กล่าวคือ อุณหภูมิของแก็สในกรณี b) จะเพิ่มขึ้น 3.97 เคลวิน ตอบ
จากตัวอย่างโจทย์ที่ผ่านมาจะพบว่า ในกรณีที่เราเปิดโอกาสให้แก็สสามารถขยายตัวได้ เมื่อให้ความร้อนเข้าไปจะทำให้อุณหภูมิของแก็สเอง เพิ่มขึ้นได้ไม่สูงนัก (เพียงแค่ 4 องศา เมื่อเปรียบเทียบกับกรณีที่ปริมาตรคงที่ ซึ่งอุณหภูมิสูงขึ้น 8 องศา) นี่ก็เพราะว่าพลังงานส่วนหนึ่งถูกนำไปใช้ทำงานในการ "ต่อสู้" กับความดันบรรยากาศภายนอก เพื่อให้แก็สขยายตัวออก จึงเหลือพลังงานเพียงบางส่วนไปกักเก็บไว้ภายใน ส่งผลให้อุณหภูมิของมันมิได้สูงขึ้นเท่าที่ควร
Keyword: กฎข้อ 1 ของเทอร์โมไดนามิกส์ , งานและความร้อน





ไม่มีความคิดเห็น:
แสดงความคิดเห็น