โดย ทีปานิส ชาชิโย
จากกฎข้อ 1 ของเทอร์โมไดนามิกส์ที่ผ่านมา [อ้างอิง 1] เราได้เห็นแล้วว่า งานที่กระทำกับระบบ เป็นปัจจัยหนึ่งที่ทำให้ระบบมีพลังงาน เปลี่ยนแปลงไป และในหัวข้อต่อไปนี้ จะได้พิจารณาในรายละเอียด ถึงขั้นตอนในการคำนวณ "งาน" ดังกล่าว ว่าเกี่ยวข้องกับสมบัติทางกายภาพ เช่น ความดัน และปริมาตร อย่างไรบ้าง
พิจารณาระบบ เช่นแก๊สที่บรรจุอยู่ภายในลูกสูบ เมื่อมีแรงลัพธ์จากภายนอก \$F\$ เข้ามากระทำ ส่งผลให้ลูกสูบหดสั้นลงเป็นระยะทาง \$ dx \$ เพราะฉะนั้น งานที่กระทำกับระบบ มีค่าเท่ากับ
อย่างไรก็ตาม ถ้าเราสมมุติให้การออกแรงบีบลูกสูบอันนี้ เกิดขึ้นไม่รวดเร็วเกินไป คือเปิดโอกาสให้ความดันในภาชนะ มีการตอบสนองต่อแรงภายนอก และกระจายความดันอย่างสม่ำเสมอทั่วทั้งปริมาตรของแก๊ส ข้อสมมุติฐานซึ่งมองว่าเหตุการณ์เกิดขึ้นอย่างช้าๆเช่นนี้ มีชื่อเรียกโดยทั่วไปว่า "Quasi-static" Quasi หมายถึง เสมือนว่า หรือ คล้ายกับว่า ในขณะที่ static หมายถึง หยุดนิ่ง
ในกรณีเช่นนี้ ความดันภายในจะออกแรงต่อลูกสูบ เพื่อตอบสนองต่อแรงภายนอกที่เข้ามากระทำ หรือ \$ P A = F \$ และเมื่อแทนเข้าไปในสมการข้างต้น จะได้ว่า
เราสามารถโยงเทอม \$ A dx \$ ในสมการข้างต้น ว่าสัมพันธ์อยู่กับปริมาตรของระบบที่มีการหดเล็กลง นั่นคือ \$ A dx = -dV \$ ให้สังเกตเครื่องหมายลบ ที่จำเป็นต้องมี กล่าวคือ เมื่อระบบมีปริมาตรหดเล็กลง เทอม \$ dV \$ โดยนิยามแล้วก็ย่อมติดลบ และ การ เติม เครื่อง หมาย ลบ เข้าไปข้างหน้าอีกครั้งหนึ่ง จะเป็นการบังคับให้ \$ - dV \$ มีค่าเป็นบวก เมื่อแก๊สโดนบีบให้ปริมาตรเล็กลง
ด้วยเหตุนี้ ทำให้เราสามารถเขียนเป็นสูตร ที่จะมีประโยชน์อย่างมากในการคำนวณ "งาน" ที่กระทำกับระบบ ว่าสัมพันธ์กับความดันและปริมาตรดังต่อไปนี้
ให้สังเกตการเขียนข้อสรุปข้างต้น ว่ามีความระมัดระวังในการใช้ภาษาอยู่มาก เพราะเงื่อนไขประกอบ มีอยู่ 2 ข้อด้วยกัน หนึ่งคือเป็นงานที่เกี่ยวข้องเฉพาะกับการขยายตัวหรือหดตัวของระบบ เช่นการขยายตัวของลูกสูบเครื่องยนต์ในจังหวะที่มีการจุดระเบิด หรือการหดตัวของลูกเทนนิสที่คุณกำลังบีบ อยู่ในมือ
แต่เราต้องเข้าใจว่า ยังมี "งาน" ในรูปแบบอื่นที่สามารถกระทำกับระบบ และส่งผลให้พลังงานของระบบมีค่าสูงขึ้น โดยมิได้เกี่ยวข้องอันใดเลย กับการที่ระบบจะหดเล็กลงหรือโป่งพองขึ้น ยกตัวอย่างเช่น การยกหนังสือ(ซึ่งเดิมวางอยู่บนพื้น)ขึ้นมาไว้บนโต๊ะ นี้ก็ถือว่าเราได้ทำงานกับหนังสือเล่มนั้น ส่งผลให้มันมีพลังงานศักย์โน้มถ่วงเพิ่มขึ้นจากเดิม เพราะตอนนี้มาอยู่บนโต๊ะ หรืออีกตัวอย่างหนึ่ง การป้อนสนามไฟฟ้าเข้าไปในแท่งโลหะ เพื่อให้อิเล็กตรอนที่อยู่ภายในเคลื่อนที่รวดเร็วมากขึ้น นี้ก็เป็นการ "ทำงาน" เช่นเดียวกัน แต่อาศัยสนามไฟฟ้า และมิได้เกี่ยวข้องอันใดเลย กับการที่ระบบจะมีปริมาตรเพิ่มขึ้นหรือลดลง
ด้วยเหตุนี้ ทุกครั้งที่เรานำสมการ \$dW = - P dV\$ มาประยุกต์ใช้ในการวิเคราะห์ จำต้องตระหนักเสมอว่า มันครอบคลุมเฉพาะ กับงานที่เกี่ยวข้องกับการบีบอัดหรือขยายตัวของระบบเท่านั้น ซึ่งหากมีกระบวนการอื่นที่เกี่ยวข้อง ก็จะต้องนำมาพิจารณาร่วมด้วย
เงื่อนไขอันที่สอง ก็คือการบีบอัดหรือขยายตัวออก จะต้องไม่เกิดขึ้นเร็วเกินไป หรือที่เรียกว่า Quasi-static ประเด็นที่จะต้องขยายความต่อไปอีกก็คือ คำว่า "เร็วเกินไป" ใช้อะไร? เป็นเกณฑ์ในการตัดสิน
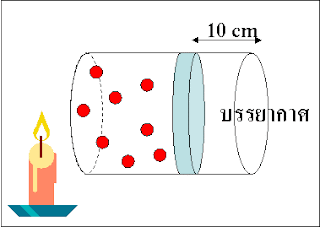
พิจารณาภาพข้างต้น ซึ่งเป็นแบบจำลองของแก๊ส ในลักษณะ Slow Motion ทำให้มองเห็นการเคลื่อนที่ของอนุภาคด้วยตาเปล่า ได้ชัดเจนยิ่งขึ้น นี้เป็นตัวอย่างของกระบวนการ Quasi-static ซึ่งเกิดขึ้นค่อนข้างช้า กล่าวคือ ในขณะที่มีการบีบให้ปริมาตรเล็กลงด้วยแรงภายนอก แก๊สที่อยู่ภายใน มีเวลาเพียงพอในการจัดเรียงและกระจายตัวตอบสนองต่อแรงภายนอก ทำให้ความดันและอุณหภูมิมีค่าเท่ากัน ตลอดทั่วทั้งภาชนะ
แต่ถ้าการบีบอัดเกิดขึ้น "เร็วเกินไป" จะส่งผลให้มีคลื่นกระแทกเกิดขึ้น และในขณะที่แนวคลื่นกำลังทะลักเข้าไปด้านในภาชนะอยู่นั้น ความดันและอุณหภูมิจะกระจายตัว ไม่ สม่ำเสมอ หากจะอธิบายความหมายของคำว่า "เร็วเกินไป" ให้ชัดเจนยิ่งขึ้น ให้คุณสังเกตคลื่นที่เกิดขึ้นภายในภาชนะ มันเคลื่อนที่ด้วยความเร็วค่าหนึ่ง เมื่อทบทวนวิชาฟิสิกส์พื้นฐานจะพบว่า คลื่นซึ่งเคลื่อนที่ในตัวกลางเช่นแก๊ส ก็คือ "คลื่นเสียง" เพราะฉะนั้น หากเรากระแทกให้ลูกสูบหดตัวลง เร็วมากกว่า ความเร็วเสียงในอากาศ นี้ย่อมถือว่า "เร็วเกินไป" และไม่จัดอยู่ในประเภท Quasi-static
การหดหรือขยายตัวของลูกสูบในรถยนต์ที่คุณนั่ง แม้จะดูด้วยตาเปล่าถือว่าเร็วมาก โดยเฉพาะเครื่องยนต์ที่รอบจัด อย่าง BMW หรือ Benz แต่เมื่อเทียบกับความเร็วเสียงในอากาศ ซึ่งอยู่ราว 300 m/s นั้นยังถือว่าช้ามาก เพราะฉะนั้น สิ่งที่เกิดขึ้นในลูกสูบรถยนต์ ยังคงถือว่าเป็น Quasi-static เพราะอย่างไรเสีย ความเร็วของลิ้นลูกสูบ ก็ยังช้ากว่าความเร็วเสียง
ตัวอย่างโจทย์
อากาศ ณ ความดันบรรยากาศ บรรจุในแท็งก์ขนาดใหญ่มาก หากต้องการทำให้ปริมาตรหดเล็กลงสัก 1 ลิตรอย่างช้าๆ จำเป็นต้อง ทำงาน กี่จูล ?
วิธีทำเนื่องจากเดิมแก๊สมีปริมาตรมหาศาล แม้เราทำให้เล็กลงอีกเพียง 1 ลิตร เราจะทำการประมาณว่า ความดันภายในถังยังคงมีค่าคงที่ นั่นคือ \$ P = 101,000 \, \text{Pascal} \$ (แม้ในทางทฤษฎีแล้วความดันจะต้องเพิ่มขึ้นเล็กน้อย) โจทย์กำหนดให้ปริมาตรเล็กลง 1 ลิตร นั่นหมายถึง \$ dV = - 0.001 \, m^3 \$ ให้สังเกตเครื่องหมายลบ ที่ปรากฎอยู่ เนื่องจากเป็นการ "หดเล็กลงของปริมาตร"
ทำการแทนค่า \$dV\$ และ \$ P \$ ในสูตรของการคำนวณหางาน ที่จะต้องทำกับระบบของแก๊ส
นั่นคือ เรา (ในฐานะสิ่งแวดล้อมภายนอก) จะต้องทำงานกับระบบ เท่ากับ +101 จูล ตอบ
ตัวอย่างโจทย์
กระบอกสูบ พื้นที่หน้าตัด 10 ตารางเซนติเมตร มีอากาศอยู่ 0.2 mol อยู่ในภาวะสมดุลกับ ความดันบรรยากาศภายนอก ถ้าถ่ายเทความร้อนเข้าไปช้าๆ แก๊สมีอุณหภูมิสูงขึ้น ในขณะเดียวกันกับที่ขยายตัวออก สมมุติพอมันพองตัวออกได้เป็นระยะทาง 10 cm ปรากฎว่ามีความร้อนเข้าไปแล้ว 20 จูล ในขณะนั้น อุณหภูมิจะเพิ่มจากเดิมเท่าใด ?
วิธีทำภาพรวมของโจทย์ข้อนี้ เราจะต้องอาศัยกฎข้อ 1 ของเทอร์โมไดนามิกส์ ทำการคำนวณพลังงานภายในของแก๊ส \$ dU \$ ที่เพิ่มขึ้น จากนั้นโยงมาถึงอุณหภูมิที่เพิ่มขึ้น โดยอาศัยความสัมพันธ์
| \$ U = \frac{3}{2}nRT \$ หรือ \$dU = \frac{3}{2}nRdT\$ | --------- (E.1) |
เริ่มด้วยกฎข้อ 1 ของเทอร์โมไดนามิกส์ ที่ว่า
| \$dU = dQ + dW\$ | --------- (E.2) |
ซึ่งโจทย์กำหนดให้ \$ dQ = 20 \, \text{J} \$ คงเหลือเพียงการคำนวณ \$ dW \$ อันเป็นประเด็นในการฝึกทำโจทย์ของข้อนี้ เนื่องจากลูกสูบสามารถขยายตัวได้ ดังนั้นมันจะขยายตัวออก เพื่อรักษาสมดุลให้ความดันภายใน มีค่าเท่ากับความดันภายนอก หรือความดันบรรยากาศเสมอ เพราะฉะนั้นในสถาะการณ์เช่นนี้ ความดันของระบบคงที่ ณ \$ P = 101000 \, \text{Pascal}\$
และเมื่อมีการขยายตัวออก \$ dV =\$ พื้นที่หน้าตัด คูณ ระยะ 10 cm \$ = 10 \, cm^2 \times 10 \, cm = 100 \, cm^3\$ หรือ
ให้สังเกตเครื่องหมายบวก เนื่องจากในกรณีนี้ ปริมาตรมีการขยายตัวออก และเราสามารถคำนวณ งานที่กระทำกับระบบได้ว่า
ซึ่งเมื่อนำเอา \$ dW \$ ย้อนกลับไปแทนในสมการ (E.2) เพื่อคำนวณหาพลังงานที่เพิ่มขึ้นของแก๊ส จะได้ว่า
จากนั้น อาศัยสมการ (E.1) เพื่อโยงความสัมพันธ์ไปยังอุณหภูมิที่เพิ่มขึ้น
กล่าวคือ อุณหภูมิของแก๊ส จะเพิ่มขึ้น 3.97 เคลวิน ตอบ
โจทย์ Hardcore
ที่มาของการคำนวณงานที่กระทำกับระบบ \$ dW = P A dx \$ ในข้างต้นนั้น เกิดจากข้อสมมุติที่ว่า การเคลื่อนที่ของลิ้นลูกสูบเกิดขึ้นอย่างช้าๆ แทบจะหมายถึงแรงลัพธ์ ที่กระทำกับมันเป็นศูนย์ นั่นคือ แรง \$ F \$ จากภายนอก สมดุลกับแรง \$ P A \$ อันเนื่องมาจากความดันภายใน หรือ \$ F = P A \$ จึงส่งผลให้ \$ dW = F dx = P A dx \$ นี้ย่อมขัดอย่างสิ้นเชิงในความเป็นจริงของลูกสูบในเครื่องยนต์ ที่ลิ้นลูกสูบเคลื่อนที่ด้วยความเร่ง และมีความเร็วสูง กล่าวคือ แรงลัพธ์ที่กระทำกับลิ้นลูกสูบย่อมไม่เป็นศูนย์ หรือ \$ F \ne P A \$ (เพราะหากแรงลัพธ์เป็นศูนย์ ลิ้นลูกสูบคงหยุดนิ่งอยู่ และไม่อาจเคลื่อนที่เข้ามาตั้งแต่แรก)
จงแสดงให้เห็นว่า แม้ \$ F \ne P A \$ งานที่กระทำกับแก๊ส ก็ยังคงเป็น \$ dW = P A dx \$ อยู่เช่นเดิม
วิธีทำ
สมมุติว่าแรงภายนอก มีค่าสูงกว่าแรงจากความดันภายในของลูกสูบ หรือ \$ F \gt PA \$ ส่งผลให้มีแรงลัพธ์กระทำกับลูกสูบ เร่งมันให้เคลื่อนที่เข้ามาภายใน อย่างรวดเร็ว หากพิจารณาในแง่ของงานและพลังงานแล้ว งานที่แรง F กระทำ ย่อม มีผลสองประการ 1 ) คือ เพิ่มพลังงานจลน์ลิ้นลูกสูบ หรือ Piston และ 2) ที่เหลือ โดนผันไปเป็นงาน ที่กระทำกับแก๊ส กล่าวคือ
| งานที่แรง F กระทำ = เพิ่มพลังงานจลน์ของ Piston + งานที่กระทำกับแก๊ส | --------- (E.1) |
ข้างซ้ายของสมการ (E.1) งานที่แรง \$ F \$ กระทำย่อมมีค่าเท่ากับ \$ F dx \$ ในขณะที่ข้างขวาของสมการ (E.1) ประกอบด้วยสองเทอม ซึ่งเราจะพิจารณาพลังงานจลน์ ที่เพิ่มขึ้น ของ Piston เสียก่อน
ในตอนแรก ลูกสูบมีความเร็ว \$ v \$ ดังนั้นมันมีพลังงานจลน์ \$ \frac{1}{2} m v^2 \$ ครั้นเมื่อเวลาผ่านไป \$ dt \$ ลูกสูบเคลื่อนที่ได้ระยะ \$ dx \$ และมีความเร็วเพิ่มขึ้น \$ dv \$ ทำให้มีพลังงานจลน์ \$ \frac{1}{2} m ( v + dv ) ^2 \$ นั่นหมายถึงพลังงานจลน์ที่เพิ่มขึ้นก็คือ
สังเกตว่า ภายในช่วงเวลาสั้นๆ \$ dt \$ นี้แรงมีค่าคงที่ เพราะฉะนั้นความเร่งภายในช่วงเวลานี้เท่ากับ \$ a =\frac{ F_\text{net} }{m} = \frac{F - PA}{m} \$ ส่งผลให้ความเร็วที่เพิ่มขึ้น \$ dv = a dt = \frac{F - PA}{m} dt \$ ดังนั้น
นอกจากนี้ ในสภาวะที่ความเร่งคงที่ ระยะกระจัด \$ dx = \frac{1}{2} a dt ^2 + v dt = v dt + \frac{1}{2} \frac{F - PA}{m} dt ^2 \$ ซึ่งก็คือเทอมในวงเล็บที่สอง(ขวาสุด)ของสมการข้างต้นพอดี เพราะฉะนั้น พลังงานจลน์ที่เพิ่มขึ้น
เมื่อแทนผลลัพธ์ข้างต้น กลับเข้าเทอมแรก ในด้านขวามือของสมการ (E.1) จะได้ทำให้
สมการข้างต้นแสดงให้เห็นว่า แม้ลูกสูบจะพุ่งเข้ามาค่อนข้างเร็วและแรง (ไม่เร็วสุดโต่งมากจนเทียบเท่าความเร็วเสียง) งานที่กระทำกับแก๊ส ก็ยังคงอยู่ในรูป \$ PA dx \$ หรือ อีกนัยหนึ่ง \$ dW = - P dV \$ ตอบ
Keyword: งานที่ใช้บีบอัด หรือ ขยายตัวของแก๊ส , W = -pdV
อ้างอิง
- [1] กฎข้อหนึ่งของเทอร์โมไดนามิกส์ https://teepanis.blogspot.com/p/blog-page.html





ไม่มีความคิดเห็น:
แสดงความคิดเห็น