โดย ทีปานิส ชาชิโย ภาควิชาฟิสิกส์ คณะวิทยาศาสตร์ มหาวิทยาลัยนเรศวร
ฟิสิกส์มัธยมปลายมีมนต์เสน่ห์ของการประยุกต์กับสิ่งที่เรามองเห็น คานงัด คานดีด คือม้ากระดกในสนามเด็กเล่น ลูกรอกใช้ดึงวัสดุก่อสร้างขึ้นตึกสูง หรือแรงเสียดทาน ใช้ออกแบบถนนให้มุมเอียงสามารถเข้าโค้งได้อย่างปลอดภัย กลศาสตร์ควอนตัม มีมนต์เสน่ห์ของการประยุกต์กับ สิ่งที่เรา มอง ไม่ เห็น (ด้วยข้อจำกัดของสายตามนุษย์ ที่ไม่ละเอียดเพียงพอ) เช่น อะตอม ที่ต่อกันเป็นโมเลกุล หรือเรียงตัวเป็นระเบียบภายในผลึก หรือ เจาะ ลึก เล็กลงไป ในนิวเคลียส เหล่านี้คืออาณาเขตที่ทฤษฎีควอนตัม แสดงศักยภาพของการทำนาย ได้อย่างเต็มที่
ศึกษาอะตอมไฮโดรเจน
ไฮโดรเจนประกอบด้วย 1 อิเล็กตรอน เคลื่อนที่อยู่ภายใต้อิทธิพลของแรงดึงดูดทางไฟฟ้าจากนิวเคลียส หากจะศึกษาให้สมจริงใน 3 มิติ เราต้องเขียนสมการ Schrödinger ของอิเล็กตรอน ให้อยู่ในรูปของ
สังเกตว่าพลังงานจลน์ใน 3 มิติ ประกอบด้วยอนุพันธ์อันดับสอง ของทั้ง 3 แกน และพลังงานศักย์ คืออันตรกิริยาแบบคูลอมบ์ แต่เนื่องจากเป็นระบบใน 3 มิติ ผลเฉลย มีความซับซ้อนเกินกว่าเนื้อหาในปัจจุบัน ดังนั้น ในเบื้องต้นเราจะใช้โมเดลอย่างง่าย ในการศึกษาอะตอมไฮโดรเจน เพราะอิเล็กตรอนถูกขังอยู่ในอะตอม ในทำนองเดียวกับที่ อนุภาคมวล \$ m \$ ถูกขังอยู่ในบ่อศักย์ ดังแสดงในภาพที่ 1a
แม้จะเป็นโมเดลอย่างง่าย แต่ก็คำนวณพลังงาน \$ E \$ ของไฮโดรเจน ได้ดีพอสมควร ในภาพ แสดงความหนาของบ่อศักย์ เท่ากับ 1 อังสตรอม เพราะนี่คือขนาดเส้นผ่าศูนย์กลาง(โดยประมาณ)ของไฮโดรเจน ในขณะที่ความสูงของขอบบ่อ ได้จากการแทน รัศมี \$ r = 0.5 \$ อังสตรอม เข้าไปในเทอมของพลังงานศักย์คูลอมบ์ \$ \frac{e^2}{4 \pi \epsilon_0} \frac{1}{r} \$ ดังแสดงในภาพ 1b ทำให้ได้โมเดล Finite Square Well ที่มีความสูง \$ V_0 = \frac{( 1.602 \times 10^{-19} )^2 }{4 \pi (8.854 \times 10^{-12} ) (0.5 \times 10^{-10}) } = 4.614 \times 10^{-18} \text{ J}\$ หรือ \$ 28.8 \text{ eV} \$
ในหัวข้อนี้ เราจะแก้สมการ Schrödinger เพื่อหาระดับพลังงาาน \$ E \$ และ ฟังก์ชันคลื่น \$ \psi(x) \$ ของ Finite Square Well ดังในภาพ 1a
ระดับพลังงาน
ในตัวอย่างโจทย์ของหัวข้อที่ผ่านมา [อ้างอิง 1] เราได้ตั้งสมการของบ่อศักย์แบบ Finite Square Well ไว้ อย่าง ครบ ถ้วน ดังนี้
| \$ \psi_{I}(x) = B_1 e^{+\kappa x} \qquad \qquad \qquad \quad \$ | (1) |
| \$ \psi_{II}(x) = A_1 sin(k x ) + A_2 cos(k x) \$ | (2) |
| \$ \psi_{III}(x) = B_2 e^{-\kappa x} \qquad \qquad \qquad \quad \$ | (3) |
โดยตัวแปร \$ B_1, A_1, A_2, B_2, k, \kappa \$ ที่มาจาก 3 บริเวณ (I), (II), และ (III) คำนวณได้จาก 6 สมการ
| \$ B_1 = A_2 \$ | (4) |
| \$ \kappa B_1 = k A_1 \$ | (5) |
| \$ A_1 sin(k L) + A_2 cos(k L) = B_2 e^{-\kappa L} \$ | (6) |
| \$ k A_1 cos(k L) - k A_2 sin(k L) = -\kappa B_2 e^{-\kappa L} \$ | (7) |
| \$ k^2 + \kappa^2 = \frac{2 m V_0}{\hbar^2} \$ | (8) |
| \$ \int_{-\infty}^0 \psi^2_{I}(x) dx + \int_0^L \psi^2_{II}(x) dx + \int_L^\infty \psi^2_{III}(x) dx = 1 \$ | (9) |
ซึ่งเมื่อคำนวณค่า \$ k, \kappa \$ ได้แล้ว ก็สามารถโยงเข้าหาพลังงานได้ว่า
| \$ k^2 = \frac{2 m E}{\hbar^2} \qquad \$ | (10) |
| \$ \kappa^2 = \frac{2 m (V_0 - E)}{\hbar^2} \$ | (11) |
เพื่อคำนวณค่า \$ k, \kappa \$ พิจารณาสมการ (8) ซึ่งมีอยู่เพียงสองตัวแปร ขั้นต่อไป เราจะต้องสร้างอีกสมการหนึ่ง ซึ่งมีเพียง \$ k, \kappa \$ ปรากฎอยู่
นำความสัมพันธ์ \$ A_2 = B_1 \$ จากสมการ (4) และ \$ A_1 = \frac{\kappa}{k} B_1 \$ จากสมการ (5) แทนเข้าในสมการ (6) และ (7) ตามลำดับข้างต้น เราแยกตัวประกอบเอา \$ B_1 \$ มาไว้ส่วนหน้า เพื่อรอการกำจัด ด้วยการเอาสมการแรก หาร สมการที่สอง
จากนั้น คูณไขว้ แล้วจัดรูป จะได้ความสัมพันธ์ดังในเฉลยการบ้านของหัวข้อที่ผ่านมา ก็คือ
| \$ (k^2-\kappa^2)sin(k L ) - 2 k \kappa cos(k L) = 0\$ | (12) |
ข้างต้น เป็นอีกสมการหนึ่ง ที่มีเฉพาะ \$ k, \kappa \$ ดังที่เราต้องการ ซึ่งเมื่อผนวกกับกราฟของวงกลม \$ k^2 + \kappa^2 = \frac{2 m V_0}{\hbar^2} \$ จะสามารถวาดกราฟ เพื่อหาจุดตัด ดังที่กล่าวไว้ ในหัวข้อที่ผ่านมา
แต่ความสัมพันธ์ \$ (k^2-\kappa^2)sin(k L ) - 2 k \kappa cos(k L) = 0\$ ยังไม่เหมาะสมที่จะวาดกราฟ (ที่แกนตั้งเป็น \$ \kappa \$ แกนนอนเป็น \$ k \$) ได้ทันที เราต้องปรับ ให้อยู่ในรูปของฟังก์ชัน \$ \kappa(k) \$ เสียก่อน
เริ่มด้วยการนำสมการ (12) มาเขียนเป็นสมการกำลังสอง \$ a \kappa^2 + b \kappa + c = 0 \$ กล่าวคือ
จากนั้น ถอดราก \$ \kappa = \frac{- b \pm \sqrt{b^2 - 4 a c} }{2 a} \$ ได้ 2 ผลเฉลย
| \$ \kappa = \frac{-k cos(k L) + k}{sin(k L)} = \quad k tan(\frac{k L}{2}) \$ | (13) |
| \$ \kappa = \frac{-k cos(k L) - k}{sin(k L)} = - k cot(\frac{k L}{2}) \$ | (14) |
ด้านขวามือสุด ของ 2 สมการข้างต้น ได้จากการนำเอกลักษณ์ \$ sin(x) = 2 sin(\frac{x}{2}) cos(\frac{x}{2})\$ และ \$ cos(x) = cos^2(\frac{x}{2}) - sin^2(\frac{x}{2})\$ ตลอดจน \$ 1 = cos^2(\frac{x}{2}) + sin^2(\frac{x}{2})\$ มาปรับใช้ให้เป็นประโยชน์
และเมื่อนำวงกลม ดังสมการ (8) มาวาดกับกราฟของสมการ (13) และ (14) จะได้จุดตัดดังแสดงในภาพที่ 2a ซึ่งเป็นกรณีทั่วไป หรือภาพที่ 2b ซึ่งเป็นกรณีของไฮโดรเจนในกรณีทั่วไป กราฟสีน้ำเงินของสมการ (13) จะตัดกับวงกลมสีแดงเป็นอันดับแรก ถัดมาทางขวา จะเป็นเส้นประสีเขียวของสมการ (14) และจะสลับกันอยู่เช่นนี้ เรื่อยไป
ภาพที่ 2b เป็นกรณีของโมเดลอย่างง่ายที่เราใช้ศึกษาไฮโดรเจน แสดงให้เห็นจุดตัด เพียงจุดเดียว ซึ่งมีพลังงาน \$ E = 11.7 \text{ eV}\$ แต่ก่อนที่เราจะเปรียบเทียบกับระดับพลังงานของไฮโดรเจน จะต้องรอบคอบ อีกขั้นหนึ่ง
ในภาพข้างต้น พลังงานที่ถูกต้อง ของไฮโดรเจน \$ E_\text{H} = -13.6 \text{ eV} \$ เป็นการรายงานผลที่ใช้ขอบบ่อ เป็นฐานในการนับศูนย์ กล่าวคือ รายงานว่า พลังงานอยู่ต่ำลงมา(ติดลบ)จากขอบบ่อ เท่ากับ \$ 13.6 \text{ eV} \$ ซึ่งแตกต่างจากวิธีการนับพลังงานของโมเดล Finite Square Well ที่เราใช้อยู่นี้ ดังนั้น เพื่อเทียบเคียงกับไฮโดรเจน เราจะต้องนำพลังงาน \$ E = 11.7 \text{ eV}\$ มา ลบ ออก จาก ขอบบ่อศักย์ \$ V_0 = 28.8 \text{ eV}\$ เพื่อหาว่าระดับพลังงาน อยู่ต่ำลงมา จากขอบบ่อเท่าใด
ซึ่งคลาดเคลื่อนอยู่ที่ประมาณ 25% ถือว่าไม่เลวนัก สำหรับโมเดลที่มีข้อจำกัด ที่รวบรัดตัดตอนอยู่บ้าง อาทิเช่น
- สมมุติให้เป็น 1 มิติ ทั้งที่ไฮโดรเจนมี 3 มิติ
- ใช้โมเดลแบบบ่อศักย์สี่เหลี่ยม ทั้งที่ไฮโดรเจนเป็นรูป โค้ง แบบคูลอมบ์
- บ่อศักย์ลึกจำกัดค่าหนึ่ง แต่ไฮโดรเจนลึกอนันต์ ณ ใจกลางของนิวเคลียส
ระบบหน่วยวัด Atomic Unit
หากนักศึกษาวาดกราฟ เพื่อตรวจสอบผลลัพธ์ในภาพที่ 2b หรือเพื่อทำการบ้าน ก็ดี จะมีความยุ่งยากพอสมควรหากใช้ระบบ SI เนื่องจาก พลังงานอยู่ในหน่วย จูล หรือ ระยะทางเป็นเมตร ซึ่งล้วนมีค่าสูงมาก เมื่อเทียบกับพลังงานหรือระยะทางในระดับอะตอม นอกจากนี้ ตัวเลขในระบบ SI ยังมี เศษ ทศนิยม เป็นอุปสรรคในการคำนวณ เช่น มวลอิเล็กตรอน \$ m_e = 9.109 \times 10^{-31} \$ กิโลกรัม หรือ ขนาดประจุของมัน \$ e = 1.602 \times 10^{-19} \$ คูลอมบ์ เป็นต้น
จินตการหน่วยวัดที่ออกแบบไว้อย่างลงตัว กับการแก้สมการ Schrödinger เหมาะกับอะตอม หรือโมเลกุล ระบบซึ่งมีค่าคงที่พื้นฐานต่อไปนี้ เท่ากับ 1 !!! พอดี
ข้างต้น คือเอกลักษณ์ของระบบ Atomic Unit ซึ่งมีหน่วยในการวัดระยะทาง พลังงาน หรือเวลา แตกต่างจากระบบ SI ดังข้อมูล ต่อไปนี้
| ระยะทาง | ใช้หน่วย Bohr | \$ \enspace 1 \text{ Bohr} = 5.291772 \times 10^{-11} \text{ m} = 0.529 \text{ angstrom} \$ |
| พลังงาน | ใช้หน่วย Hartree | \$ \enspace 1 \text{ Hartree} = 4.359745 \times 10^{-18} \text{ J} = 27.211 \text{ eV}\$ |
| เวลา | ไม่มีชื่อเฉพาะ | \$ \enspace 1 \text{ Unit of Time} = 2.418884 \times 10^{-17}\text{ s}\$ |
การบ้าน
จงเขียนสมการ Schrödinger ของไฮโดรเจนใน 3 มิติ ด้วยระบบ Atomic Unit
เฉลย\$ -\frac{1}{2}(\frac{d^2 \psi}{d x^2} + \frac{d^2 \psi}{d y^2} + \frac{d^2 \psi}{d z^2} ) - \frac{1}{r}\psi = E \psi \$
การบ้าน
จงเปลี่ยนความหนา \$ L = 1 \text{ angstrom} \$ และ ความสูง \$ V_0 = 28.8 \text{ eV} \$ ให้อยู่ใน Atomic Unit
เฉลย \$ L = 1.89 \text{ Bohr} \$ และ \$ V_0 = 1.058 \text{ Hartree} \$
ทั้งนี้ ไม่ว่านักศึกษาจะเลือกใช้ระบบ SI หรือ Atomic Unit ก็ตาม เพื่อความไม่ประมาท ควรให้ตัวแปรที่เกี่ยวข้องทุกตัวในสูตรนั้นๆ หรือในกราฟนั้นๆ เป็นระบบเดียวกัน
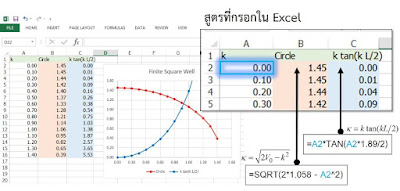
ภาพที่ 4 แสดงการวาดกราฟด้วยโปรแกรม Excel ด้วยระบบ Atomic Unit โดยใช้ \$ L = 1.89 \text{ Bohr} \$ และ \$ V_0 = 1.058 \text{ Hartree} \$ ซึ่งจะได้ค่า \$ k = 0.929 \text{ Bohr}^{-1} \$ และคำนวณพลังงานได้ว่า (สังเกตความสะดวกในการใช้ \$ \hbar = 1 \$ และ \$ m = 1 \$)
จากนั้นเราค่อยเปลี่ยนหน่วยของพลังงานที่คำนวณได้ ให้กลายเป็น \$ \text{eV} \$ หรือ \$ \text{Joule} \$ หรือ \$ \text{Calorie} \$ เพื่อการรายงานผล เพื่อวาดภาพ วาดกราฟประกอบการนำเสนอผลงาน ตามแต่รสนิยมและวัฒนธรรมการเลือกใช้หน่วยวัด ของแต่ละสาขาวิชา
ฟังก์ชันคลื่น
จากการวาดกราฟในหัวข้อที่ผ่านมา เมื่อทราบค่า \$ k \$ เป็นที่เรียบร้อย เราสามารถคำนวณ \$ \kappa = \sqrt{ \frac{2 m V_0}{\hbar^2} - k^2} \$ และตัวแปรที่เหลือ \$ B_1, A_1, A_2, B_2 \$ ได้ทั้งหมด ทำให้ได้ฟังก์ชันคลื่น \$ \psi(x) \$ ที่สมบูรณ์ เพื่อวิเคราะห์ต่อยอดไปถึง \$ |\psi(x)|^2 \$ ซึ่งแสดงลักษณะการกระจายตัวของกลุ่มหมอกอิเล็กตรอน ภายในบ่อศักย์
กล่าวอีกนัยหนึ่ง \$ B_1, A_1, A_2, B_2 \$ ล้วนเป็นฟังก์ชันของ \$ k, \kappa \$ ส่วนจะมีรูปแบบทางคณิตศาสตร์เช่นใดนั้น รายละเอียดอยู่ในการบ้านต่อไปนี้
การบ้าน Hardcore
จงใช้สมการ (4)-(9) เพื่อเขียน \$ B_1, A_1, A_2, B_2 \$ ให้เป็นฟังก์ชันของ \$ k, \kappa \$
บอกใบ้ เขียนตัวแปร \$ A_1, A_2, B_2 \$ ให้อยู่ในรูป \$ B_1 \$ จากนั้นใช้หลักการ Normalization จากสมการ (9) เพื่อคำนวณ \$ B_1 \$ นอกจากนี้ ใช้สมการ (12) จัดรูป \$ B_1 \$ ให้แลดูสวยงาม
เฉลย\$ \quad \begin{split} B_1(k,\kappa) &= \sqrt{ \frac{2 k^2 \kappa }{(k^2 + \kappa^2)(\kappa L + 2)}} \cr A_1 &= \frac{\kappa}{k} B_1 \cr A_2 &= B_1 \cr B_2 &= \left[ \kappa sin(k L)+ k cos(k L) \right] \frac{e^{\kappa L}}{k} B_1\cr \end{split} \$
ภาพที่ 5 แสดงลักษณะทั่วไปของฟังก์ชันคลื่น ซึ่งสืบเนื่องมาจากภาพ 2a ที่เราได้คำนวณค่า \$ k, \kappa \$ ไว้ก่อนหน้านี้ และนำมาคำนวณ \$ B_1(k,\kappa), \enspace A_1(k,\kappa), \enspace A_2(k,\kappa), \enspace B_2(k,\kappa) \$ เพื่อสร้างเป็นฟังก์ชันคลื่น ของแต่ละพื้นที่ (I), (II), (III) จากนั้นนำมาวาดบนกราฟ
ตรวจสอบด้วยสายตา สังเกตว่าฟังก์ชันคลื่น แบ่ง ออก เป็น 2 ประเภท คือ 1) มีความสมมาตรรอบกึ่งกลางบ่อ ในลักษณะของฟังก์ชันคู่ (แสดงด้วยสีน้ำเงิน) และประเภทที่ 2) มีความปฏิสมมาตร หรือที่เรียกว่า ฟังก์ชันคี่ (แสดงด้วยสีเขียว) และเพื่อชี้ให้เห็น ในประเด็นความสมมาตรอันนี้ เราจะทำตัวอย่างโจทย์อีกข้อหนึ่ง ที่วางตำแหน่งของบ่อศักย์ให้สมมาตรรอบจุดกำเนิด กล่าวคือ บ่อศักย์อยู่ในบริเวณ \$ -\frac{L}{2} \lt x \lt +\frac{L}{2} \$ แล้วจะนำผลลัพธ์ที่ได้ มาวิเคราะห์ในประเด็นนี้อีกครั้ง ภายหลังจากตัวอย่างโจทย์ ต่อไปนี้
ตัวอย่างโจทย์
จงหาฟังก์ชันคลื่น และระดับพลังงานของ Finite Square Well ดังแสดงในภาพ
เราแบ่งพื้นที่ออกเป็น 3 บริเวณเช่นเคย แต่เนื่องจากความสมมาตรของบ่อศักย์ ที่เป็นตัวกำหนดธรรมชาติการเคลื่อนที่ของอนุภาค เราใช้ตรรกะว่า
สังเกตเครื่องหมาย ยกกำลังสอง ที่แสดงถึงความน่าจะเป็นที่จะพบอนุภาค จากนั้นวิเคราะห์ต่อไปอีกว่า การที่ ฝั่งซ้าย-ฝั่งขวา ของฟังก์ชัน \$ \psi(x) \$ จะ ยก กำ ลัง สอง แล้วมีค่าเท่ากัน หรือ สมมาตร กันนั้น ย่อมเกิดขึ้นได้สองลักษณะ คือ
ฝั่งขวา = -ฝั่งซ้าย หรือเรียกว่า ฟังก์ชันคี่
- ภาพ ก) แสดงดัวอย่างฟังก์ชันคู่ ที่ ทั้ง สอง ฝั่ง มีค่าเท่ากัน อาทิเช่น ฟังก์ชัน พาราโบล่า \$ f(x) = x^2 \$ หรือ \$ cos(x) \$
- ภาพ ข) แสดงตัวอย่างฟังก์ชันคี่ ที่ทั้งสองฝั่ง มีเครื่องหมาย กลับกัน เช่น ฟังก์ชันแปรผันตรง \$ f(x) = 2x \$ หรือ เส้นโค้งแปรผกผัน \$ \frac{1}{x}\$ และที่สำคัญ \$ \quad sin(x) \$
ด้วยเหตุนี้ เราจะสร้างผลเฉลย \$ \psi_{I}(x), \enspace \psi_{II}(x), \enspace \psi_{III}(x) \$ แยกคนละประเภท
ประเภทฟังก์ชันคู่ หลังจากเขียนสมการ Schrödinger ในแต่ละบริเวณ เราสร้างผลเฉลยได้ว่า
| Even solutions \$ \qquad \displaylines{ \psi_{I}(x) = B e^{+\kappa x} \quad \cr \psi_{II}(x) = A cos(k x) \cr \psi_{III}(x) = B e^{-\kappa x} \quad } \$ | (E.1) |
บริเวณตรงกลาง เราเลือกเฉพาะ \$ cos(k x) \$ เพราะมันเป็นฟังก์ชันคู่ ส่วนบริเวณขอบบ่อซ้ายขวา มีสัมประสิทธิ์ \$ B \$ เหมือนกันทั้งคู่ เพราะเรากำหนดให้มันเป็นฟังก์ชันคู่ แปลว่า ทั้งซ้ายและขวา จะต้องมีขนาดสมมาตรกัน หรือ เท่ากัน
เมื่อนำ \$ \psi_{II}(x) \$ และ \$ \psi_{III}(x) \$ มา "เย็บต่อกัน" ณ รอยต่อ \$ x = +\frac{L}{2} \$ จึงเกิดเป็น 2 สมการ
จับทั้งสองสมการ หารกัน จะได้ว่า
| Even solutions \$ \qquad \kappa = k tan(\frac{k L}{2}) \$ | (E.2) |
ซึ่งได้ผลลัพธ์อันเดียวกัน กับสมการ (13) นี้เป็นว่า มันจะต้องให้พลังงาน ค่าเดียวกัน นั่นเอง
นอกจากนี้ เรายังสามารถใช้หลักการ Normalization เพื่อคำนวณค่า \$ A, B \$ ได้ว่า
| Even solutions \$ \qquad A = \sqrt{\frac{2 \kappa}{\kappa L + 2}}; \quad B = A cos(\frac{k L}{2}) e^{\frac{\kappa L}{2}} \$ | (E.3) |
ประเภทฟังก์ชันคี่ ผลเฉลยอยู่ในรูป
| Odd solutions \$ \qquad \displaylines{ \psi_{I}(x) = B e^{+\kappa x} \quad \cr \psi_{II}(x) = A sin(k x) \cr \psi_{III}(x) = -B e^{-\kappa x} \quad } \$ | (E.4) |
ให้เทียบสมการ (E.1) กับสมการ (E.4) ว่าคราวนี้ เราเลือกใช้ \$ sin(k x) \$ แทน เพราะเรากำลังพิจารณาฟังก์ชันคี่ ในขณะที่ขอบซ้ายขวา สัมประสิทธิ์ \$ B \$ มีเครื่องหมายสลับกัน ซึ่งเป็นเอกลักษณ์ของฟังก์ชันคี่ และเมื่อพิจารณารอยต่อ \$ x = +\frac{L}{2} \$ จะนำไปสู่สมการ
| Odd solutions \$ \qquad \kappa = - k cot(\frac{k L}{2}) \$ | (E.5) |
เช่นเคย ได้ผลลัพธ์เดียวกันกับสมการ (14) นี้เป็นว่ามีระดับพลังงานเท่ากัน และสุดท้าย ใช้หลัก Normalization เพื่อหาค่า \$ A, B \$
| Odd solutions \$ \qquad A = \sqrt{\frac{2 \kappa}{\kappa L + 2}}; \quad B = -A sin(\frac{k L}{2}) e^{\frac{\kappa L}{2}} \$ | (E.6) |
ฟังก์ชันคลื่น แบ่งออกเป็น 2 ประเภท คือ ฟังก์ชันคู่ และ ฟังก์ชันคี่ ส่วนพลังงานที่ได้ มีค่าเท่าเดิม ตอบ
จากการวิเคราะห์ตัวอย่างโจทย์ที่ผ่านมา ทำให้ทราบว่า แม้เราวางตำแหน่งของบ่อศักย์ให้สมมาตรรอบจุดกำเนิด \$ -\frac{L}{2} \lt x \lt +\frac{L}{2} \$ ระดับพลังงานที่คำนวณได้ กลับมีค่าไม่ต่างจากกรณี \$ 0 \lt x \lt L \$ ดังในภาพ 1a
พฤติกรรมอันนี้ เกิดจากที่ทั้งสองกรณี ไม่ได้แตกต่างกันอย่างมีนัยะสำคัญ เป็นแต่เพียงทางเลือกของการวางระบบพิกัดที่แตกต่างกัน เท่านั้นเอง
แต่การใช้ตรรกะความสมมาตรเข้ามาช่วย ก็ทำให้กระบวนการทางคณิตศาสตร์ในตัวอย่างโจทย์ ลด ความ ซับ ซ้อน ลงไปมาก ทั้งยังสามารถจำแนกประเภทของฟังก์ชันคลื่นออกมาได้ชัดเจน โดยความสัมพันธ์ \$ \kappa = k tan(\frac{k L}{2}) \$ ดังสมการ (13) เป็นฟังก์ชันคู่ และ \$ \kappa = - k cot(\frac{k L}{2}) \$ ดังสมการ (14) เป็นฟังก์ชันคี่ ซึ่งหากรู้อย่างนี้ ชะรอยเราวางบ่อศักย์ให้สมมาตรตั้งแต่แรก คงจะเป็นการดี
การบ้าน Hardcore
ให้ \$ n_\text{even} \$ และ \$ n_\text{odd} \$ เป็นเลขจำนวนเต็ม ที่แสดงจำนวนสถานะ Bound State ของกรณีฟังก์ชันคู่ และ คี่ ตามลำดับ จงพิสูจน์ว่า
หมายเหตุ วิศวกรสามารถใช้ความสัมพันธ์ข้างต้น ออกแบบจำนวนสถานะที่ต้องการ ด้วยการปรับ ความหนา หรือความสูงของบ่อศักย์ให้เหมาะสม ยกตัวอย่างเช่น ถ้าเป็นกรณีอิเล็กตรอน \$ m = m_e \$ และเลือก \$ L = 4 \text{ Bohr}, \enspace V_0 = 2 \text{ Hartree}\$ มีผลให้ \$ \frac{L \sqrt{2 m V_0}}{2 \pi \hbar} = \frac{4 \sqrt{2 \times 1 \times 2}}{2 \pi \times 1} = 1.273 \$ หรือ
\$ n_\text{odd} \le 1.773 \enspace \$ แปลว่า \$ \enspace n_\text{odd} = 1 \enspace \$ (จำนวนเต็มที่ไม่เกิน 1.773)
บอกใบ้ พิจารณาภาพที่ 2a) จุดตัดระหว่างวงกลม \$ k^2 + \kappa^2 = \frac{2 m V_0}{\hbar^2} \$ กับสมการ (13) หรือ (14) จะต้องเกิดขึ้น ทางขวา ของจุดที่ \$ \kappa \$ เท่ากับศูนย์
ตัวอย่างโจทย์ Hardcore
พิจารณา Double Well Potential ดังแสดงในภาพ เมื่อ \$ R \$ คือระยะห่าง ระหว่างจุดศูนย์กลางของ 2 บ่อ โดยแต่ละบ่อ มีความกว้าง \$ L \$ จงหาความสัมพันธ์ ระหว่าง \$ k \$ และ \$ \kappa \$ (เพื่อใช้ในการคำนวณพลังงาน ในลำดับต่อไป)
ขั้นตอนการคำนวณโดยละเอียด อาจใช้กระดาษทดถึง 10 หน้า ดังนั้นเราจะอธิบายพอสังเขป
อาศัยความสมมาตรของบ่อศักย์ เราแบ่งการวิเคราะห์ออกเป็น ฟังก์ชันคู่ และ คี่
ประเภทฟังก์ชันคู่ เขียนฟังก์ชันคลื่นออกมาได้ว่า
ณ รอยต่อ \$ x = \frac{R}{2} - \frac{L}{2}\$ สร้างได้ 2 สมการ
นำสมการล่าง หารด้วย สมการบน เพื่อกำจัดตัวแปร \$ F \$ แต่ก่อนอื่น เรานิยามตัวย่อ เพื่อประหยัดเวลาในการทด และ ลด ความผิดพลาดจากอาการตาลาย
นำสมการล่าง หารด้วย สมการบน จะได้ \$ \kappa t = \frac{k A_1 C_- - k A_2 S_-}{A_1 S_- + A_2 C_-} \$ แล้วจัดรูป
| \$ A_1[\kappa t S_- - k C_-] = - A_2 [ \kappa t C_- + k S_- ] \$ | (E.1) |
ณ รอยต่อ \$ x = \frac{R}{2} + \frac{L}{2}\$ สร้างได้อีก 2 สมการ
นำสมการล่าง หารด้วย สมการบน จะได้ \$ - \kappa = \frac{k A_1 C_+ - k A_2 S_+}{A_1 S_+ + A_2 C_+} \$ คูณไขว้ แล้วแยก \$ A_1, A_2 \$ ออกมาไว้ เพื่อรอการกำจัด
| \$ A_1[\kappa S_+ + k C_+] = - A_2 [ \kappa C_+ - k S_+ ] \$ | (E.2) |
กำจัด \$ A_1, A_2 \$ ด้วยการหาร สมการ (E.1) ด้วย (E.2) เกิดเป็น \$ \frac{\kappa t S_- - k C_-}{\kappa S_+ + k C_+} = \frac{\kappa t C_- + k S_-}{\kappa C_+ - k S_+} \$ คูณไขว้ แล้วจัดรูป
| \$ (k^2 - \kappa^2 t)[S_+ C_- - S_- C_+] - k \kappa (t + 1)[ S_- S_+ + C_- C_+] = 0\$ | (E.3) |
อาจต้องใช้ความอดทนเล็กน้อย แต่เราพิสูจน์ได้ว่า \$ [S_+ C_- - S_- C_+] = sin(k L)\$ และ \$ [ S_- S_+ + C_- C_+] = cos(k L) \$ ดังนั้น เราได้ความสัมพันธ์ของ \$ k, \kappa \$ กรณีฟังก์ชันคู่ ก็คือ
| Even solutions \$ \quad (k^2 - \kappa^2 t) sin(k L) - k \kappa (t + 1) cos(k L)= 0\$ | (E.4) |
ประเภทฟังก์ชันคี่ เขียนฟังก์ชันคลื่นออกมาได้ว่า
ณ บริเวณตรงกลาง \$ \psi_{III} \$ จะต้องเป็นฟังก์ชันคี่ จึงต้องอยู่ในรูป \$ ( e^{+ \kappa x } - e^{- \kappa x } ) \sim sinh(\kappa x) \$ ส่วนในบริเวณของ \$ \psi_{IV} \$ หรือ \$ \psi_{V} \$ ไม่สามารถใช้ความเป็นฟังก์ชันคี่ มาร่วมพิจารณา เพราะมันไม่ได้อยู่ตรงกลาง ไม่จำเป็นต้องมีลักษณะ "ปฏิสมมาตร" ซ้ายขวา แต่อย่างใด
และหากสร้างสมการ ณ รอยต่อทั้งสอง จากนั้น กำจัดตัวแปร \$ F, A_1, A_2, B \$ ให้เหลือเพียง \$ k, \kappa \enspace \$ ในกรณีฟังก์ชันคี่จะได้ว่า
| Odd solutions \$ \quad (k^2 t - \kappa^2) sin(k L) - k \kappa (t + 1) cos(k L)= 0\$ | (E.5) |
ได้ความสัมพันธ์ของฟังก์ชันคู่และคี่ ดังสมการ (E.4) และ (E.5) ตามลำดับ ตอบ
แอบมองเนื้อหา Quantum Tunnelling
ฟังก์ชันคลื่นในหัวข้อที่ผ่านมา ซ่อนไว้ด้วยความลึกลับทางควอนตัม ที่ไม่เคยปรากฏมาก่อนในฟิสิกส์ยุคดั้งเดิม กล่าวคือ เมื่อสังเกตการเคลื่อนที่ของวัตถุขนาดใหญ่ หากมันมีพลังงาน \$ E \$ ไม่เพียงพอที่จะเอาชนะบ่อศักย์ \$ V_0 \$ ที่ขังมันไว้ภายใน ก็จะไม่สามารถหลุดออกไปข้างนอกได้เลย ตัวอย่างมีให้เห็นอยู่ทั่วไป ดาวเคราะห์ของระบบสุริยะ ถูกขังอยู่ในบ่อศักย์เนื่องจากแรงโน้มถ่วงของดวงอาทิตย์ และจากหลักฐานทางธรณีวิทยากว่า 4.5 พันล้านปีที่โลกของเราถือกำเนิดขึ้น มันไม่เคยหลุดออกจากวงโคจรไปได้ ค่อยๆสาวไม้คิวแล้วแทงลูกสนุกเกอร์เบาๆ มันก็ไม่มีทางกระโดดข้ามขอบโต๊ะสักหลาดออกไปได้ เช่นกัน
เมื่อวัตถุขนาดเล็ก ถูกขังอยู่ภายในบ่อศักย์ มันกลับมีความน่าจะเป็นที่จะหลุดออกไปข้างนอก ดังแสดงในภาพที่ 5 พิจารณาฟังก์ชันคลื่นที่ได้จากสมการ Schrödinger จะเห็นว่า แม้เลยออกมานอกบ่อแล้ว ฟังก์ชันคลื่นก็ยังไม่เป็นศูนย์ แต่จะลดลงเรื่อยๆ แบบ Exponential Decay และในเมื่อฟังก์ชันคลื่น \$ \psi\ne 0 \$ ก็ย่อมแสดงว่า ความน่าจะเป็น \$ \psi^2 \$ ไม่เท่ากับศูนย์ ด้วยเช่นกัน
ภาพที่ 6 แสดงพฤติกรรมที่อนุภาคสามารถทะลุทะลวงเข้าไปในอาณาเขต ของ ขอบบ่อ ทั้งๆที่มันมีพลังงานไม่เพียงพอ เริ่มจากภาพด้านซ้ายมือ คือกรณีของ Finite Square Well
ภายในบ่อ ฟังก์ชันคลื่นมีการสั่นขึ้นลง คล้ายคลื่น ที่มีแอมปลิจูดคงที่ค่าหนึ่ง นี้เกิดจากลักษณะทางคณิตศาสตร์ของ \$ \psi(x)\$ ที่อยู่ในรูป \$ cos(k x) \$ หรือ \$ sin(k x) \$ เลื่อน มา ทางขวามือ ตามแนวแกน \$ x \$ จะเข้าสู่บริเวณขอบบ่อ \$ x = 4 \$ ซึ่ง \$ E \lt V_0 \$ ในบริเวณนี้ \$ \psi(x) \ne 0 \$ และจะค่อยๆลดลงแบบ \$ e^{-\kappa x } \$
จะเกิดอะไรขึ้น? ถ้าขอบบ่อ ขาดแหว่งออกไป
คำตอบดังแสดงในภาพที่ 6(ขวา) คือ กลาย เป็น "กำแพงศักย์" ไม่ได้มีลักษณะของ บ่อ อีกต่อไป ในกรณีนี้ ฟังก์ชันคลื่นวกกลับมาสั่นขึ้นลงอีกครั้ง ในทางคณิตศาสตร์ นี้เป็นผลจากการแก้สมการ Schrödinger ในบริเวณที่ \$ V = 0 \$ ดังที่เราได้วิเคราะห์แล้วในบทที่ 1 [อ้างอิง 2]
ปรากฎการณ์ในภาพที่ 6(ขวา) เรียกว่า Quantum Tunnelling หรือ การทะลุทะลวงเชิงควอนตัม ที่ลำอนุภาค เคลื่อนที่เป็นสาย คล้ายลำน้ำที่ฉีดออกจากท่อ เข้าปะทะกำแพงศักย์ และแม้พลังงานจลน์ที่ถูกฉีดเข้ามาในตอนต้นจะสู้ความสูงของกำแพงศักย์ไม่ได้ อนุภาคก็ยังสามารถ เล็ดลอดทะลุกำแพงออกไป
การจะแก้สมการ Schrödinger ของกำแพงศักย์ จะต้องมีความเข้าใจเรื่อง เวลา ดีพอสมควร เพราะอนุภาคมีการเลื่อนตำแหน่งเมื่อเวลาผ่านไป และที่สำคัญ มีโมเมนตัมเป็นสมบัติเฉพาะตัว เราจะต้องทราบวิธีการสร้างฟังก์ชันคลื่น(จำนวนเชิงซ้อน!)ที่สะท้อนพฤติกรรมดังกล่าวของอนุภาค ซึ่งจะต้องรอในบทที่ 3 "เวลา และ โมเมนตัม" แต่หัวใจสำคัญของปรากฏการณ์ Tunnelling ซุกซ่อนอยู่ใน Finite Square Well ที่เรากำลังเรียนอยู่นี้ เท่านั้นเอง
จงหาความน่าจะเป็น ที่อนุภาคจะอยู่นอกบ่อ
พิจารณาบ่อศักย์ ที่บังเอิญอนุภาคมีพลังงานในสถานะพื้น \$ E = \frac{V_0}{2} \$ เพื่อความสะดวก เราจะวางบ่อศักย์ให้สมมาตร แล้ววาดกราฟของฟังก์ชันคลื่น \$ \psi \$ ตลอดจน \$ \psi^2 \$ ดังแสดงในภาพที่ 7
จากภาพ เมื่อ \$ x \in [L/2,\infty)\$ ฟังก์ชันคลื่น \$ \psi(x) = B e^{-\kappa x}\$ นอกจากนี้ ภาพที่ 7(ขวา) แสดง "ความหนาแน่นของความน่าจะเป็น" หรือ \$ \psi^2 \$ ซึ่งมีพื้นที่ใต้กราฟ \$ 2 \int^{\infty}_{L/2} \psi^2 dx \$ หมายถึงความน่าจะเป็นที่อนุภาคจะอยู่นอกบ่อ สังเกตว่าเราอินทิเกรตเฉพาะซีกขวามือ แล้วค่อยคูณด้วย 2 เพราะ \$ \psi^2 \$ มีความสมมาตร ซ้ายขวา
| ความน่าจะเป็น ที่อนุภาคจะอยู่นอกบ่อ = \$ 2 \int^{\infty}_{L/2} \left( B e^{-\kappa x} \right)^2 dx \$ | (\$ E = \frac{V_0}{2}) \$ |
จากตัวอย่างโจทย์ที่ผ่านมา เราทราบว่า \$ A = \sqrt{\frac{2\kappa}{\kappa L+2}}\$ และ \$ B = A cos(k L/2) e^{\kappa L /2}\$ จึงแทนเข้าไปเพื่อคำนวณความน่าจะเป็น
| \$ 2 \int^{\infty}_{L/2} \left( B e^{-\kappa x} \right)^2 dx = 2 B^2 \underbrace{ \int^{\infty}_{L/2} e^{-2 \kappa x} dx }_{\frac{1}{2 \kappa}e^{-\kappa L}}= \frac{2 }{\kappa L + 2} cos^2(k L/2) \$ | (\$ E = \frac{V_0}{2}) \$ |
ขั้นต่อไป เราเพียงหาค่า \$ k, \kappa \$ เพื่อนำมาคำนวณความน่าจะเป็นข้างต้น อาศัยความสัมพันธ์ \$ E = \frac{V_0}{2}\$ แทนเข้าในสมการ (10) จะได้ว่า
| \$ k^2 = \frac{2 m E}{\hbar^2} = \frac{m V_0}{\hbar^2} \$ | (\$ E = \frac{V_0}{2}) \$ |
และใช้สมการ (11) เพื่อคำนวณ \$ \kappa \$
| \$ \kappa^2 = \frac{2 m V_0}{\hbar^2} - k^2 = \frac{m V_0}{\hbar^2} \$ | (\$ E = \frac{V_0}{2}) \$ |
นี้เป็นว่า \$ \kappa = k \$ และจาก \$ \kappa = k tan(\frac{k L}{2}) \$ ในสมการ (13) แสดงว่า \$ tan(\frac{k L}{2}) = 1\$ ซึ่งโดยเอกลักษณ์ของตรีโกณมิติแล้ว \$ tan(45^\circ) = 1 = tan(\frac{\pi}{4}) \$ ดังนั้น
| \$ \frac{k L}{2} = \frac{\pi}{4} \$ หรือ \$ k L = \frac{\pi}{2} = \kappa L \$ | (\$ E = \frac{V_0}{2}) \$ |
แทน \$ k L = \frac{\pi}{2} = \kappa L \$ เข้าไปในความน่าจะเป็น ที่เราคำนวณค้างไว้ จะได้ว่า
| \$ 2 \int^{\infty}_{L/2} \left( B e^{-\kappa x} \right)^2 dx = \frac{2 }{\kappa L + 2} cos^2(k L/2) = \frac{2 }{\pi/2 + 2} cos^2(\pi/4) \$ | (\$ E = \frac{V_0}{2}) \$ |
สุดท้ายได้ข้อสรุป ก็คือ
| ความน่าจะเป็น ที่อนุภาคจะอยู่นอกบ่อ \$ = \frac{2}{\pi + 4} \approx 28\% \$ | (\$ E = \frac{V_0}{2}) \$ |
มีความน่าจะเป็นถึง 28% !!! ปรากฏการณ์เช่นนี้ ไม่เคยมีมาก่อนในกลศาสตร์คลาสสิก !? เพราะถ้าเป็นอย่างนั้น โลกของเราคงกระโดดออกไปอยู่นอกระบบสุริยะ เป็นเวลาอย่างน้อย 3 เดือนใน 1 ปี แต่ในทางกลศาสตร์ควอนตัม กลับสามารถเป็นไปได้ (สำหรับอนุภาคที่มีขนาดเล็กเช่นอิเล็กตรอน)
ถ้าเป็นบ่อศักย์ทั่วๆไป อาจมีความน่าจะเป็น น้อยลงกว่านี้บ้าง โดยเฉพาะถ้าบ่อลึกมากๆจนยากที่อนุภาคจะทะลวงออกไป ตัวอย่างข้างต้นเป็นกรณีศึกษาที่คำนวณได้ชัดเจนและมีผลลัพธ์ออกมาเป็นเทอมที่เรียบง่าย เพียงพอในการแสดงประเด็นของ Quantum Tunnelling กล่าวคือ การที่ \$ E \lt V_0 \$ จะทำให้ผลเฉลยของสมการ Schrödinger อยู่ในรูป Exponential Decay หรือ \$ e^{-\kappa x}\$ ยิ่งทะลวงล้วงลึกเข้าไปเท่าไหร่ ก็ยิ่งลดลงไป มากเท่านั้น แต่ไม่เท่ากับศูนย์ จึงมีโอกาสที่อนุภาคจะไปปรากฏตัว อยู่นอกบ่อศักย์ นั่นเอง
มากไปกว่านั้น ปรากฏการณ์ Quantum Tunnelling ยังถูกนำมาสร้างกล้องจุลทรรศน์กำลังขยายสูง ที่ส่องเห็นได้แม้กระทั่งอะตอม เรียกว่า Scanning Tunnelling Microscope อันเป็นงานชิ้นโบว์แดงระดับรางวัลโนเบลสาขาฟิสิกส์ในปี 1986 ซึ่งเราจะได้ศึกษาในรายละเอียด ในบทที่ 3 กันต่อไป
สรุป
เราได้ศึกษาบ่อศักย์แบบ Finite Square Well ซึ่งในภาพรวม มีหลักในการตั้งสมการ ไม่ต่างจากเดิมที่ผ่านมา คือ แบ่งบ่อศักย์ออกเป็นส่วนๆ, หาคำตอบทีละส่วน, แล้วนำมา "เย็บต่อกัน"
เป็นการสะดวก ที่เราจะวางบ่อศักย์ให้สมมาตร \$ -\frac{L}{2} \lt x \lt +\frac{L}{2} \$ ซึ่งจะได้ฟังก์ชันคลื่น ใน 2 ลักษณะ คือฟังก์ชันคู่ และ ฟังก์ชันคี่ โดยที่ทั้งสอง มีความสัมพันธ์ \$ \kappa = k tan(\frac{k L}{2}) \$ และ \$ \kappa = - k cot(\frac{k L}{2}) \$ ตามลำดับ
ในการคำนวณระดับพลังงาน จะต้องใช้การวาดกราฟ เพื่อหาค่า \$ k \$ ที่เหมาะสม แล้วนำมาคำนวณต่อยอด เป็นพลังงาน หรือ เป็นฟังก์ชันคลื่น แต่หากจะคำนวณให้ สะดวก ขึ้นไปอีก เราอาจใช้ระบบ Atomic Unit ที่วัดระยะทางเป็น Bohr และ พลังงานเป็น Hartree
สุดท้าย นำมาประยุกต์เพื่อศึกษาอะตอมไฮโดรเจน โมเดลอย่างง่ายที่เราใช้ ให้ผลลัพธ์ของพลังงานเท่ากับ \$ E_H^{\text{(Model)}} = -17.1 \text{ eV}\$ เทียบกับค่าจริง \$ E_H= -13.6 \text{ eV}\$ ก็นับว่าไม่เลวนัก แม้เป็นโมเดลที่มีข้อจำกัดอยู่หลายประเด็น
จากที่เกริ่นไว้ในตอนต้น ว่ามนต์เสน่ห์ของควอนตัม อยู่ที่การประยุกต์ใช้กับสิ่งที่เรา มองไม่เห็น และในหัวข้อต่อไป เราจะได้ศึกษาพันธะเคมีของโมเลกุลอย่างง่ายที่สุดในเอกภพ นั่นคือ \$ \text{H}_2 \$ ด้วยโมเดลของบ่อศักย์แบบ Double Well Potential ที่ได้ปูพื้นทางคณิตศาสตร์ไว้แล้วในตัวอย่างโจทย์ที่ผ่านมา ตลอดจนบ่อศักย์แบบ Dirac Delta อันเป็นรูปแบบที่พบบ่อยครั้ง ในกลศาสตร์ควอนตัม
ด้วยรักและผูกพัน, ทีปานิส ชาชิโย
Keyword: กลศาสตร์ควอนตัม, อะตอม ไฮโดรเจน, Finite Square Well, Double Potential Well
อ้างอิง
- [1] หัวข้อที่ 1 "Semi-Finite Square Well" บทที่ 2 https://teepanis.blogspot.com/2018/03/semi-finite-square-well.html
- [2] หนังสือ "กลศาสตร์ควอนตัมระดับอุดมศึกษา" https://sites.google.com/site/siamphysics/intro-quantum/online-textbook









ไม่มีความคิดเห็น:
แสดงความคิดเห็น